StripeMerge shows a method to merge narrow stripes to wide stripes.
motivation
Wide stripes ($\frac{n}{k}$ is close to 1) can help cold data in EC schema to a better redundancy. But in production, there are more narrow stripes. So how to generate wide stripes from narrow one without extreme re-construction costs?
from logical viewpoints, we want to combine 2 narrow stripes with $(k, m)$ to 1 wide stripe with $(2k, m)$. But we have to spread all chunks to different nodes to keep EC characteristics.
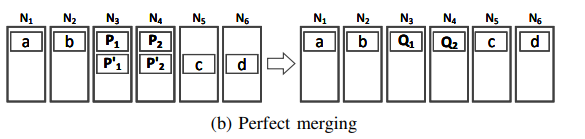
the easiest case is perfect merging showing above. Locations of all data chunks are static before and after merging. So the bandwidth usage during merging is minimized to zero!
But how to search those perfect candidates?
methods
They use bipartite graph to model this matching process. Every stripe is a node in this graph. But the time complexity of the maximum matching algorithm is too large, about $O(n^{2.5})$.
greedy
Making all merging perfect is hard, so they relax contraints. A pair with non-zero merge cost (bandwidth usage during merging) is also acceptable.
Sort all choice space by merge cost, and do merge greedyly can help reduce algorithm complexity.
parity-aligned
Use a hashmap to records paritiy chunk locations of all stripes:
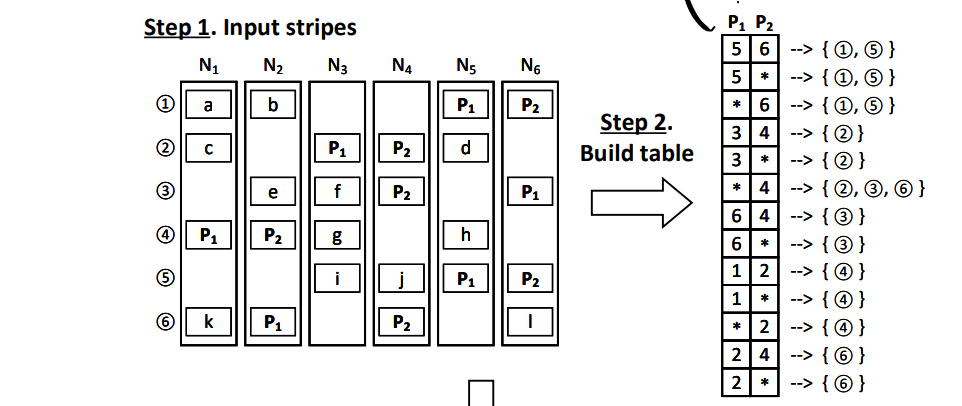
take 2 parity chunks as an example. hashmap's keys are P1+P2, and values are stripe indexes.
keep this hashmap as a part of metadata, then you can use this table and get some pairs by a given merge cost.
this hashing is like a pre-process, transferring sorting cost from the time of merging to the time of placing chunks.
Also, this method ignores the cost of transferring data chunk. But experiments show that it's negative effection is subtle.
experiments
some details…
ref
- Yao, Qiaori, et al. "StripeMerge: Efficient Wide-Stripe Generation for Large-Scale Erasure-Coded Storage." ICDCS 2021.
- X. Zhang, Y. Hu, P. P. Lee, and P. Zhou. Toward optimal storage scaling via network coding: From theory to practice. In Proc. of IEEE INFOCOM, pages 1808–1816, 2018.