Intro

For preparing for the next coming exam, Machine Learning in 2019 Spring, I wrote this article down to mark and share some insights about basic mahcine learning methods, including KNN, Perceptron, Naive Bayes(MLE, MAP), Logistic Regression, Linear Regression, SVM.

Basic Idea

Basically, machine learning is trying to use known data to predict unknown data. Supervised or unsupervised learning is depend on if any label is paired with data.

Hypothesis classes is the set of possible classification functions you’re considering.

Loss function (Objective function)

It is your model’s target, which will decide the final goal of your model and provide learning gradient. Common loss functions are zero-one loss(1 as penalty), square loss, absolute loss and etc.

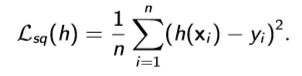
No free lunch rule

Need to make some assumptions or bias to find the best method. As a result, there is no any method that can handle all problems.

Train/Test split

It is used to test your model’s score. Similarly, valid data is split to validate your model during trainning without getting your model learn from test data.

KNN

K-Nearest Neighbor algorithm is a lazy online learning classification method based on the assumption that the most common label amongst is the input’s label. As $n \to \infty$, this method becomes accurate and slow (high memory requirement, $O(nd)$).

Distance

A general version is $dist(x,z) = (\sum_{r=1}^{d}|x_{r}-z_{r}|^p)^{1/p}$, when p = 1 -> ManhattanDistance, p = 2 -> EuclideanDistance, $p \to \infty$ -> ChebyshevDistance

Choose K

Large->reduce noise, small->less distinct. Use cross validation or Bayes method to choose this hyperparameter. It’s usually an odd number.

1-NN

The error of 1-NN is not more than twice than Bayes Optimal. 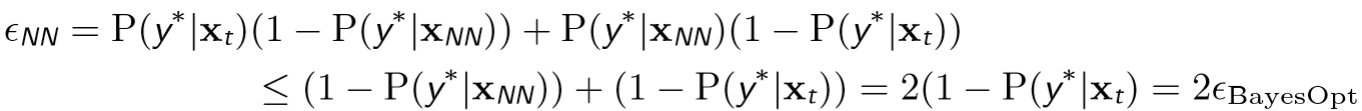where $P(y^\star|x_t)=P(y^\star|x_{NN})$

Curse of Dim

Distance of samples in high dimensional space is too big to even search whole space.
What about the hyperplanes?
Solution: Dimensional reduction, numerosity reduction, data compression…

Perceptron

Perceptron is a linear binary classifier searching a linear hyperplane to seperate binary classes data.

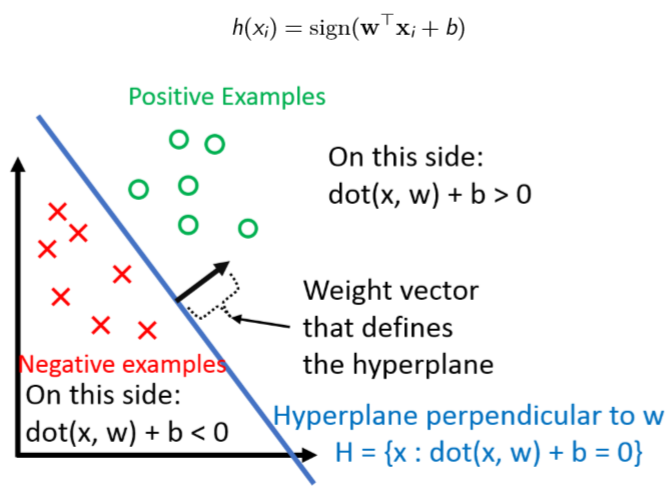
Algorithm Process:

Perceptron uses SGD to optimal loss function ($J(\theta) = - \sum\limits_{x_i \in M}y^{(i)}\theta \bullet x^{(i)}$).
So $\frac{\partial}{\partial \theta}J(\theta) = - \sum\limits_{x_i \in M}y^{(i)}x^{(i)}$ becomes $\theta = \theta + \alpha y^{(i)}x^{(i)}$.

Convergence

Naive Bayes

Bayes is a non-linear classification method. Naive Bayes’ assumpation is all conditions (features) are irrelevant (that’s why naive), so that based on the join distribution of data learned from training dataset, we can get output Y with MAP from input X.

B is category and A is feature. So we can find the highest posterriori probability of B’s category.

Generative Model & Discriminative Model

The difference of these models is the way to obtain $P(X,Y)$. The formmer estimates the join distribution of X&Y and use Bayes methods. The latter estimate $P(Y|X)$ directly.
For example, LR is discriminative (GD), and Bayes methods are generative.

MLE (Maximum Likelihood Estimation)[parameter]

• MLE gives the explanation of the data you observed.
• If n is large and your model/distribution is correct (that is H includes the true model), then MLE finds the true parameters.
• But the MLE can overfit the data if n is small. It works well when n is large.
• If you do not have the correct model (and n is small) then MLE can be terribly wrong!
• Statics.

MAP (Maximum a Posterriori Probability Estimation)[random variable]

Add a prior knowledge item to estimate $\theta$, for coin example, $\hat{\theta}=\frac{n_H+m}{n_H+n_T+2m}$. With data increasing, MAP becomes MLE, but when sample size is limited, it would be a significant change.

As a result, we change the target from MLE’s $log[P(D;\theta)]$ to $log[p(D;\theta)]+log[P(\theta)]$. The added item is independent of the data and penalizes if the parameters, θ deviate too much from what we believe is reasonable.

Ture Bayesian

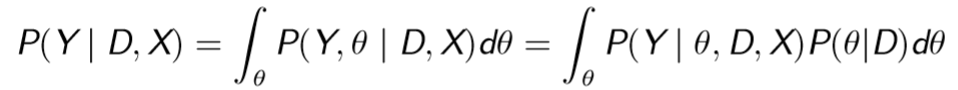
It’s intractable.

Linear Regression

Linear Regression: $f(x) = \sum_{m=1}^{p}w_{m}x_{im}+w_{0}=w^{T}x_{i}$

Loss function: $J(w)=\frac{1}{n} \sum_{i=1}^{n}(y_{i}-f(x_{i}))^{2}$.

it can be also derived from MLE.

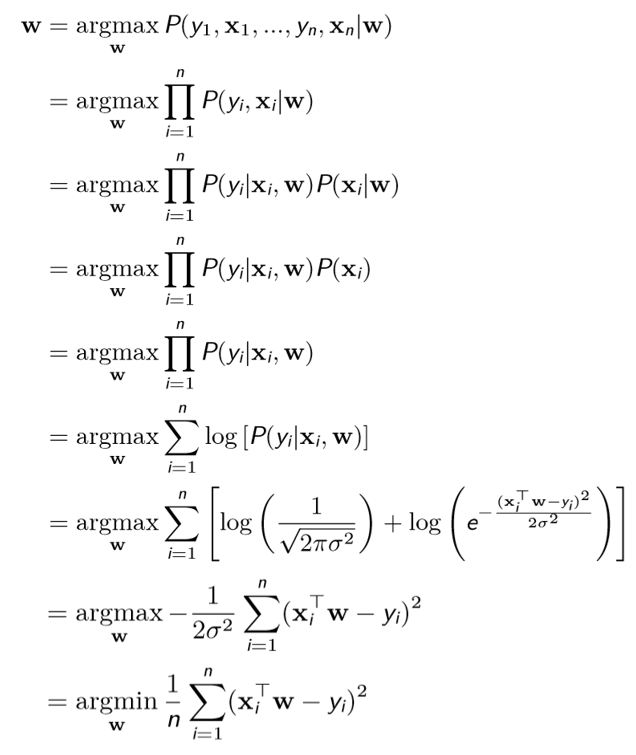
When it comes to MAP.

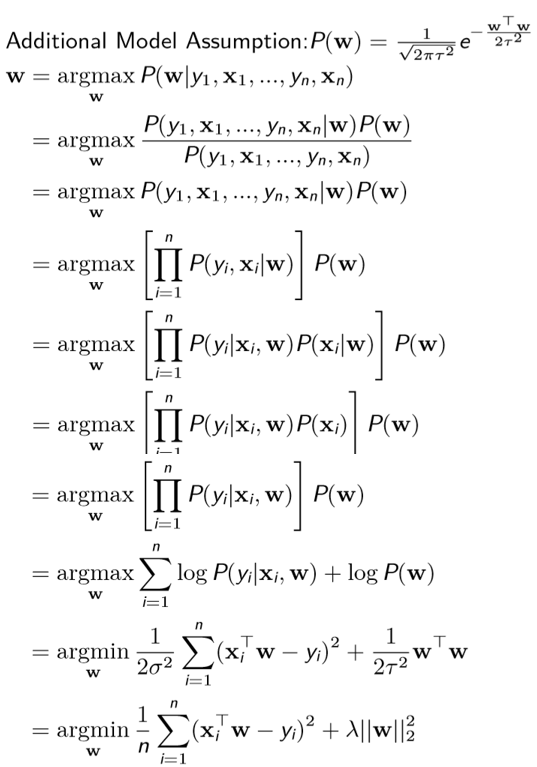
Logistic Regression

LR uses sigmoid function ($\frac{1}{1+e^{-Z}}$) to output classification probability, but still is are linear method drawing a linear hyperplane.
Use gradient decent (Partial derivative) to optimal MLE loss:

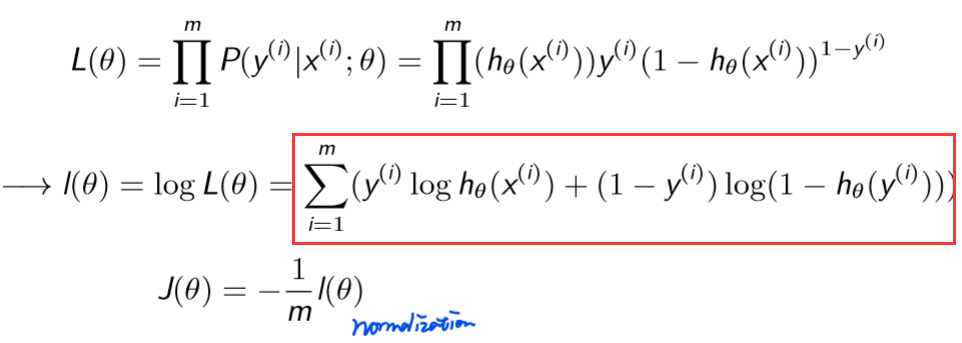
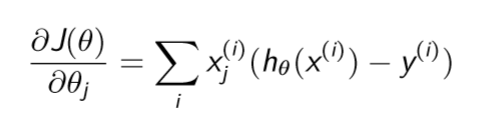
It looks like add an activation function to linear regression, what’s more, optimal methods can achieve the global maximum point by this convex loss function.

L2 Regularization

$\sum_{j=1}^{n}\theta^{2}_{j}$ is used to prevent weights become too large and finally simplify this model. Use a hyperparameter to weight this item and add to the loss function.

SVM

Support Vector

To make sure all samples are not only seperated by hyperplane but also away from hyperplane. The distance between two hyperlaones is $\frac{2}{|w|_2}$.

When training SVM, those samples not in support vectors are useless for changing support vectors.

Target

Find a hyperplane with max margin $max \;\; \gamma = \frac{y(w^Tx + b)}{|w|_2}$ [distance from point to hyperplane].
Linear SVM uses hinge loss $\ell(y) = \max(0, 1-y \cdot \hat y)$, to maximum the margin, so the numerator part would be 1 and the target is $min \;\; \frac{1}{|w|_2} \;\; s.t \;\; y_i(w^Tx_i + b) \geq 1$.

Soft SVM (Slack Variable)

Change the target to $min \;\; \frac{1}{|w|^2}+C\sum_{i=1}^{m}\zeta_{i} \;\; s.t \;\; y_i(w^Tx_i + b) \geq 1-\zeta_{i}, \zeta_{i} \geq 0$, wheren C is a hyperparameter and $\zeta$ is for soft 1-constraint。

Also, there is a L2 version.

Why do I write in English?
Practicing my shitty writing skill.